IPP has much to contribute toward our understanding of nuclear structures. IPP's defect-pair concept of hadrons reveals a plausible mechanism for the strong force, as simply the mutual cancellation of a portion of their residual expansion/contraction distortion, when two defect-pairs have suitable geometric alignments (please see "8. Defect-Pair Bonding" in the HADRON TUTORIAL). This concept of the strong force permits us to infer that nucleons cluster together in essentially rigid geometric patterns, knit together by a matrix of both types of strong-force bonds.
In 3-D nuclear drawings, protons will be represented in the two ways shown below:
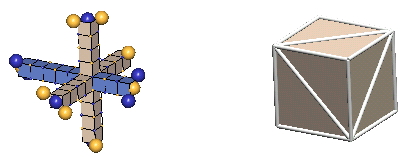 |
 |
The left forms, which IPP terms "the lattice form", are used only where the complete dynamics of the nuclear charge exchange cycles are shown (limited in this tutorial to 1H2, 1H3, 2He3, & 2He4). This form has the virtue of showing the nucleon relationships in a fully scaled manner.
The forms in the right column, which IPP terms "the cube form", are used in all the rest of the nuclei. This form has the virtue of simplicity, so one can readily see how the centers of the component nucleons relate to each other geometrically. We hope that you will learn enough about the intricacies of the charge-exchanging nucleon interactions from the our few examples in the lattice form to be able, ultimately, to perceive these simple cube forms as if they were embellished by these charge-exchanging complexities.
There is cogent evidence that both slant directions of these T-slant forms are equally represented in Nature. The best evidence for this conclusion is found in the interchanging of proton & neutron identities in the two-state charge-exchange cycle of the alpha particle, where opposite slant nucleons are required to permit ring-diagonal bonds to join them together. To see this, click here. Our conclusion: every nuclear structure we draw would be equally valid if all its defect-pair slants were reversed. IPP terms these alternative slant forms, "slant isotopes".
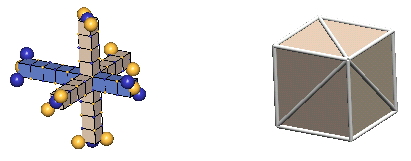
In 3-D nuclear drawings, neutrons will be represented in the two ways shown below:
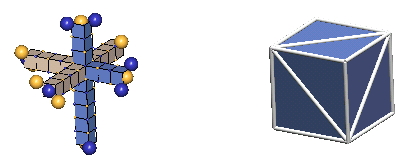 |
 |
There are subtle clues (the most convincing being the absence of a stable Helium 5) that neutrons (and, hence, protons) exist only in the T-slant form. We surmise that the M-slant form is unstable, and is found only in certain kaon resonances, and in the "core" c-void configurations of baryon resonances like sigma & xi hyperons (& a few others).
Only one strong-force bond can occur between any two nucleons. Whether this strong-force bond is a diagonal bond or a paraxial bond is determined by the geometric orientation of the two nucleons. Only one defect-pair in each nucleon is involved in forming this bond, and whether the bond is attractive, or repulsive, is determined by the slants of the associated defect-pairs. We show these relationships below:
Repulsive diagonal bonds do not form in single-plane nuclei, but do occur (along with a slight excess of attractive diagonal bonds) between nucleons in adjacent planes in multi-plane nuclei. Repulsive paraxial bonds are not found in nuclei, but obviously act during the nucleon clustering process to prevent the acquisition of protons (and neutrons) whose slant is opposite to those already existing in the nucleon cluster.
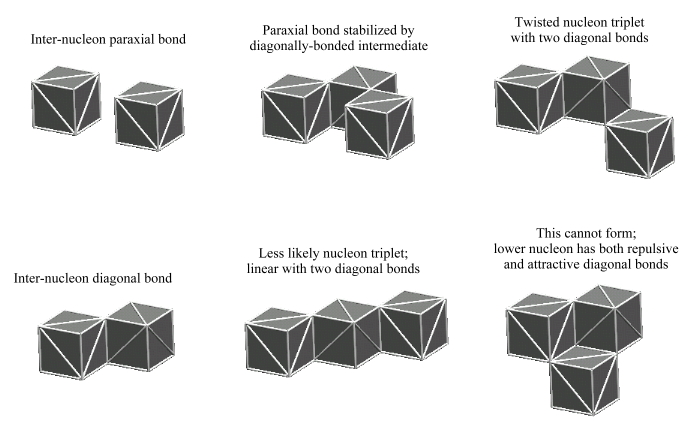
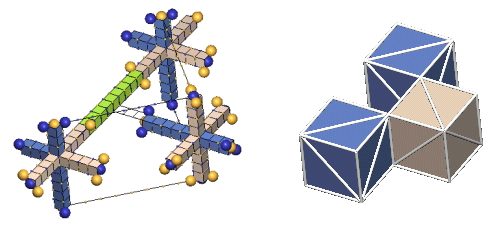
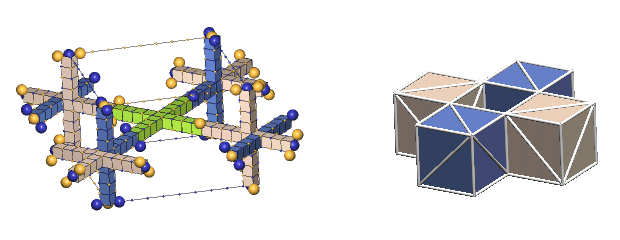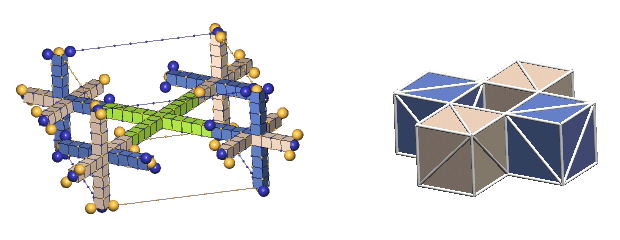
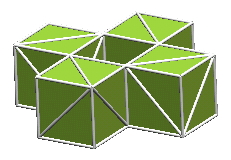
In considering how to maximize the number of bonds between nucleons in a cluster, one almost immediately sees that this can be accomplished best by compact arrangements in which all the nucleons lie in a common plane. This geometry maximizes the number of nucleons that are surround on all sides by other nucleon, whereby these "enclosed" nucleons develop the maximum number of shared bonds. However, other thoughts intrude on this simple approach:
These questions bounce endlessly around in one's mind, as one tries to find a plausible structure for a specific isotope of a specific element.
Showing the structures of large nuclei is possible only through greatly simplifying the way we represent protons and neutrons. The most common simplification will be to show the nucleons as colored cubes to indicate the type of nucleon, along with diagonal white lines on each face showing the direction of the axes of expansion of the six c-voids comprising the three orthogonal nucleon defect-pairs. However, if we compare a "cube" nuclear structure to the equivalent "defect-pair" structure, much information is obviously missing. There is no spacing information, either of the component defect-pairs, or of the bond spacings. Also, nothing is conveyed about nucleon charge exchanges, nor of changing bond spacings due to translation of the nucleus through the lattice. You will have to supply this information from your growing knowledge of nuclear dynamics.
Further simplification, even beyond the "cube" form of nucleons, is often useful in making comparisons between alternative structural possibilities. One way is to show just the top view, where nucleons are represented simply as colored squares, each with a diagonal white line to show the direction of the axis of expansion. Since nucleons exist only in T-slant form, you can obviously infer the slants of the other five faces from just this one slant line. When these top views are used to represent multiple plane nuclei, each colored square represents a vertical column of either two, or three, spaced-apart nucleons, depending upon its position in the matrix. If a column is incompletely filled, numerals are affixed to that square to indicate the plane(s) that is(are) occupied.
Even further simplification is sometimes used, when, for example, we use a matrix of normal font characters to pass information to 3-D drawing programs. We will bring these up at the appropriate time.
IPP's notion of strong-force bonds yields equations for calculating their mass-deficits, so we can often discriminate amongst various imagined structures for nuclei by seeing which has a calculated mass-deficit closest to the experimental value. Of course, these calculations are burdened by the need to consider the changing bond parameters due to the continuing synchronized* charge-exchanges of the constituent protons and neutrons, as well as possible spacing changes brought on by the nuclide's translation through the space lattice, so, currently, these calculations are feasible only for simple nuclei. Much creative effort will be required into the way these dynamics play out in large nucleon clusters, before large nuclear structures can be validated by bond calculations.
Even without the ability to accurately calculate their mass-deficits, one can often create plausible structures for large nuclei simply by hunting for nucleon arrangements that exhibit maximum numbers of bonds along with maximum nucleon pairing opportunities, and minimum numbers of weakly bonded nucleons. When you click on "Nuclei" under "VISUAL IMAGES", you will find dozens of nuclear structures arrived at through this type of reasoning. As you study these, you will discover that IPP sees pairing as a structural concept, whereby paraxially-bonded protons (or neutrons), which are equidistant from the cluster's center of mass, adopt mirror-image charge-exchange sequences. This mirroring increases their bond mass-deficits and causes their nucleon spins to be opposite and canceling.