Richard L. Ropiequet (Jan 2004)
ഀPublished in "Infinite Energy" magazine - September/October 2004 issue
ഀ ഀ ഀIn this paper, I introduce new intellectual tools that let you visualize nuclei & nuclear reactions as 3-D structures & 3-D structural modifications. These tools should be particularly useful for those of you who have engineering type minds, who need to visualize how something is constructed, and how it moves & works, before you are satisfied that you understand it. I will show you how to use these new visual approaches to gain new insights into the "NR" part of "LENR (Low Energy Nuclear Reactions)". I will also show you a new way of looking at photons and particles that perhaps clarifies the nature of "zero-point energy" and "free energy". I will investigate the following items:
ഀ ഀMy new tools let us speculate about a possible scenario by which this transmutation may be accomplished. We suppose that electrolysis creates a flood of very compact neutral proton hydrinos of low drift velocity that are gently attracted to thorium's five plane nuclear structure, where they find dozens of very weak binding sites that let them attach without provoking an immediate internal transition. However, ultimately so many attach that the nuclide becomes unstable, and undergoes rearrangement; this results in multiple smaller nuclei, because the n/p ratio is now too low for stable large nuclei.
ഀ ഀThese demonstrations utilize new insights that I have acquired about nuclei in developing a new theoretical approach to particle physics during the last thirty-two years. These insights involve the structural aspects of the bonds that join nucleons to each other, and the way in which these bonding aspects influence the specific geometrical configurations that x-protons & y-neutrons assume as they jockey for positions that maximize their individual bonding potentials. I hope to make these insights clear to you as we proceed, but prepare yourself for a mind-bending experience, because I must teach you the rudiments of an approach to particles and nuclei that literally turns conventional physics inside out.
ഀ ഀ ഀMy theory, Infinite Particle Physics (hereafter IPP), is a structural, rather than a mathematical, approach to the physics of the microcosm. The virtue of this change of focus is that it permits one to investigate the mechanisms of physical phenomena, an activity for which mathematics is unsuited. The normal fault of this change of focus is that it often leads to worthless blue-sky speculations that are incapable of corroboration by physical experiments. But this blue-sky aspect is not inevitable. With luck, one can find a key that opens the lock to Nature's mysteries. I stumbled across this crucial idea in 1971, in the form of a "collapsed-void distortion pattern" in the space lattice.
ഀ ഀThis pattern made clear the nature of the strong force, and provided a building-block concept for hadron particles and nuclei, namely, a "defect-pair", which is a space lattice structure of two collapsed lattice void defects joined together by mutual cancellation of their pattern's expansion and contraction aspects. The "defect-pair" idea proved to be much more satisfying than the current quark notion of QCD, for three very significant reasons:
ഀ ഀSpace: IPP's fundamental premise is that space is a polycrystalline solid, filled with equal numbers of ±1/2e charge particles. IPP calls these particles, "elemental charge entities", or, more commonly, "ECEs". ECEs of both polarities are considered to be rigid spheres, all of the same precise size, about 0.2 fermi (IPP's concept for a proton provides cogent evidence for this figure). It is an essential requirement of my theory to presume that ECEs exert local positioning influences upon each other, specifically that like-charge ECEs repel each other, and that unlike-charge ECEs attract each other, or at least are indifferent to each other's proximity. We must also assume that opposite-polarity ECEs do not annihilate each other when in contact, and that ECEs possess a quality akin to inertia to explain the finite velocity of light.
ഀ ഀThe source of raw material and the process of manufacture of ECEs is, of course, beyond human comprehension, but where they are injected into the universe is relevant to a successful ether theory. IPP postulates that ECEs are continuously produced & injected at the centers of all the universe's galaxies. This assures that ECEs will ultimately be forced into contact everywhere, and, with continuing production, will occur in such excess that the simple-cubic lattice of space will be squeezed out of shape and assume a rhombic character. IPP calls this universal squeezing, "shrinkage". Upon reflection, one perceives that universal shrinkage has these four aspects:
ഀ ഀMass-Energy: Distortion patterns that capture shrinkage have no natural boundaries, so any mass-energy associated with these distortion patterns must be distributed throughout the whole of space to infinity. This insight lets us see that a phenomenon's captured mass-energy is proportional to the amount of shrinkage its distortion pattern requires. Hence, IPP concludes that mass-energy = shrinkage, and we understand, then, why mass-energy is always conserved, because universal shrinkage is inherently conserved.
ഀ ഀ"Particles": IPP's concept of a "particle" (whether photon, lepton, hadron, or nucleus) is a point-centered, endlessly-extending oscillation in the packing-density of ECEs. (Note: from here on I shall use the word "particle" without quotes, but please adjust your mental image to conform to IPP's definition).
ഀ ഀThe shape of a particle's packing-density oscillation is invariably ellipsoidal, and its degree of ellipticity correlates with the drift speed of its center through the space lattice. The pulsating shape of a photon's oscillation is smooth and undistorted, while the pulsating shapes of oscillations associated with other particles are invariably distorted, due to the local ECE charge-imbalance effects, and ECE displacement effects, that clusters of lattice defects create at the oscillator's center (You will find my explanation of why & how lattice defects are bound to oscillator centers on my website).
ഀ ഀ******************************************************
ഀ ഀYou will need quite a few more of IPP's concepts to understand my presentation about LENR, but you should now be ready for my investigation #1: "How mass-energy is manifest in space". You will perceive that when the mass-energy of phenomena is viewed as forever-extending oscillations in the packing density of ECEs, these oscillations are ever-present, everywhere in the universe. Slowing a particle to zero velocity in space, i.e., cooling it to absolute zero, merely changes the shape of its oscillatory waveform from ellipsoidal to spherical, but the oscillation continues.
ഀ ഀWe may logically infer that these oscillations emanate from the centers of every phenomena in the universe, and spread in all directions in inverse-square fashion. This suggests that every point in the infinite space lattice is the recipient of inverse-square decremented information from all phenomena that have been in existence long enough for their wavefronts to have reached that point. We can also reason that all arriving wavefronts will sum vectorily at each instant, so that placing a suitable ultra-low capacitance probe in some point in space, and viewing its output with an ultra-high frequency oscilloscope, we would discover a very complex waveform, whose peak amplitude would vary according to the intensity, proximity, direction, frequency, and relative motion of surrounding phenomena.
ഀ ഀSo, how does one extract mass-energy from this bubbling ferment of ECE packing-density oscillations? Energy extraction depends upon the probability that the phases and peak amplitudes of these summation waveforms will differ at separated probe points at each instant of time, and, of course, upon the cleverness of someone able to create apparatus that turns these amplitude and phase differences into useful work.
ഀ ഀWhere would this extracted mass-energy come from? It seems most probable that it would come from reducing the frequency of the matter-waves of surrounding matter, i.e., decreasing the momentum of surrounding particles. From IPP's perspective, this would be equivalent to decreasing the ellipticity of all the oscillators contributing to these extracted ECE packing-density wave fluctuations.
ഀ ഀYou will understand why these oscillator wave-shape changes occur, if you reflect upon the manner in which a packing-density oscillation is sustained. Successive oscillatory cycles depend upon outgoing shrinkage being periodically reflected radially backward toward the oscillator center, and this has to occur throughout the oscillator's endlessly-extending pattern. Any change, anywhere, in this pattern of reflected shrinkage will ultimately affect the radial distribution of outgoing shrinkage from the oscillator's center. (By the way, this is the underlying concept of IPP's explanations of fields and forces, whose details you will find on my website. No force "particles", like vector photons, gravitons, gluons, or magnetons are needed by IPP).
ഀ ഀWhat can we infer about the magnitude of peak lattice oscillations at various sampling locations? Reason would tell us that these peak oscillations should be particularly strong near the surfaces of large solid bodies, moving rapidly through the space lattice, e.g., at the surface of the earth. It would seem self-evident that the ellipticities of all the packing-density oscillations associated with all the nuclei of the earth's matter would have to be nearly identical, with common direction of their major axes, if the earth is to move without breaking apart. IPP's concept of black-body radiation suggests that the earth moves through absolute space at approx. 370 km/s (sun's velocity relative to black-body radiation) <± 30 km/s (earth's orbital velocity) <± 0.46 km/s (its equatorial velocity).
ഀ ഀWould adequate propulsion be available anywhere in space, as some would-be galactic explorers have suggested? This seems to me to be most doubtful, because I can't perceive how large transient ECE density fluctuations could occur in the vector summation patterns of extremely distant oscillation sources. But perhaps you can, so don't let me spoil your fun!)
ഀ ഀNow, continuing my basic lecture:
ഀ ഀ ഀThe mass-energy of all these oscillatory phenomena is strictly proportional to the amount of shrinkage each has captured. The rest mass-energy of a lepton or hadron is determined by the amount of shrinkage (i.e., the amplitude of ECE packing-density oscillation) that is required to fracture the lattice sufficiently to produce the defects that lie at its center, plus enough extra shrinkage to supply momentum adequate to separate this cluster from its opposite-polarity (anti-matter) twin to sufficient distance that they lose interest in each other.
ഀ ഀThe way this cluster of defects moves through the space lattice is for each defect to slide into an adjacent lattice site, either forward or backward, always choosing a site closest to its drifting oscillator's center. This happens each time the oscillator center arrives at its rarefaction phase. Collapsed voids actually uncollapse into simple voids in this phase. This is illustrated in animated fashion in the website's "Hadron Tutorial".
ഀ ഀI could explain much more of IPP's insights, particularly about its concepts of fields and forces, and the creation and decay of matter. All of these insights would, in some small measure, improve your understanding of the transmutation of nuclei, but another time, and another place! We must return to a few more basics:
ഀ ഀ ഀThe space-lattice defects that lie at the oscillatory centers of leptons and hadrons are of four types: voids, replacements, excesses, and collapsed voids, each occurring in two polarities.
ഀ ഀThe first three defect types are found only at lepton centers:
ഀ ഀThe fourth defect type, collapsed-void defect (c-void), is found only at hadron centers:
ഀ ഀHadron particles, as I have already mentioned, are comprised of clusters of paired collapsed voids (hereafter, "c-voids"), which IPP calls, "defect-pairs". Defect-pairs are bound together by mutual cancellations of the expansion & contraction distortion that c-voids manifest when the central area of their associated packing-density oscillation is in its close-packed phase, which IPP calls "saturation" (you can view a three-dimensional animation of this saturation phenomenon in the "Introductory Tutorial" of my website).
ഀ ഀThe collapse of a void creates a distortion pattern that is symmetrical about a cardinal plane of the space lattice. Defect-pairs can form only by mutual cancellation of their respective expansion & contraction attributes, and this requires that their planes of symmetry are parallel, spaced apart, and with their centers lying in cardinal directions from each other, and with their expansion axes in "crossed", or perpendicular relationship. These pairing requirements are what let us see that the spacings between paired c-void defects are always integral numbers of lattice units, i.e., they are quantized. (Please see "Hadron Tutorial" on my website, for clarification).
ഀ ഀIn the early years of my investigation, I found a satisfying procedure for determining the defect spacings of the defect-pairs of pions, kaons, and nucleons in both their neutral and charged forms. These spacings varied from 5ü to 10ü (ü = lattice constant of the space lattice ≈ 0.2 fermi). Knowing these spacings, and having the experimental mass-energies of these particles, and reasoning that the mass-energy of defect-pairs should be proportional to the square of their defect spacings, I found an equation that accurately calculated the mass-energies of defect-pairs from 5ü to 10ü, which plausibly extrapolated out to spacings of 15ü.
ഀ ഀThese accurate mass-energy values vs. spacings permitted me to tease out the structures of all the well-known mesons and baryons, and corroborate them by comparing my calculated values to the experimental values. These were frequently within ±0.01%. These speculations also let me determine the numbers of defect-pairs in these resonances. Here is a sample of these numbers: pions=1, kaons=2, nucleons=3, sigmas=4, D's=4, xi's=5, omega=6, J/psi=8, B's=8, upsilons=16, etc. These calculations also allowed me to discover the specific spacings of the defect-pairs that are utilized in these particles. These spacings varied from 5ü to 15ü.
ഀ ഀ ഀNucleons are comprised of three mutually orthogonal defect-pairs, whose defect spacings average approx. 9ü. The six defects comprising these three defect-pairs have charges of ±1/2e, the proton having four plus and two minus charges, the anti-proton having four minus and two plus charges, while the neutron has three of each. These six charges may be visualized as sitting in the centers of the six faces of a cube. What lends stability to these two types of nucleons is a process that IPP terms "a six-state charge-exchange cycle", which allows the charges of a nucleon to circulate, such that each face assumes a sequence of alternating charges.
ഀ ഀThe proton sequence is + + + + – – ; the neutron sequence is + + + – – – . These sequences, of course, have different phases among the six faces of the cube, and the consequence of these repetitive charge migrations is to produce the integrated effect of nearly spherical charge symmetry. Another effect is to cause the defect spacings of the x, y, & z defect-pairs to vary in some characteristic way among these three possibilities, 8ü↔9ü↔10ü, depending upon the specific lattice orientation of the charge-exchange geometry.
ഀ ഀThese spacing changes affect the strength of strong-force bonds between adjacent nucleons over the six-state charge-exchange cycle, and make their calculation quite tedious, and increasingly uncertain for larger nuclide clusters, because the bond spacings may "breathe" in-and-out at different times as the nuclide moves through the space lattice, or because there may be subtle E/C cancellations due to neighboring bond interactions. Variations in bond spacings, albeit difficult to characterize, do offer a prospect for understanding excited nuclear states as increases in bond spacings. We infer that nuclides can absorb additional mass-energy simply by increasing certain of their bond spacings in some quasi-stable way, perhaps by altering charge-exchange patterns. We should understand that increased bond spacings can change only in ways that preserve bond geometry, and only in multiples of ü, so excited states are always quantized.
ഀ ഀ ഀIPP's concept of the strong force depends upon the same notion of expansion/contraction cancellation (hereafter, "E/C" cancellation) that binds the two c-voids of a defect-pair together. One sees that this E/C cancellation between any defect-pair's paired c-void defects can't be 100%, because the two c-voids are spaced apart. Therefore the lattice at each end of a defect-pair will manifest a minute residue of the unpaired c-void's E/C pattern at that end. Since these weakened E/C patterns extend outwardly from every one of a nucleon's six c-voids, we can see the possibility that nucleons can interact with each other's residual E/C patterns to incur further E/C canceling, provided that they move into "suitable alignments" with each other. This E/C canceling reduces the mass-energy required to support the two nucleons, so mass-energy is given off in the interaction, typically as a gamma. This release of mass-energy binds the two defect-pairs together, and the amount of this gamma's mass-energy correlates with the inter-nucleon bond's mass-deficit.
ഀ ഀIPP provides equations for calculating the mass deficits of individual inter-nucleon bonds. These equations were derived, not from nuclear mass deficit information, but, rather, from my attempts to find appropriate structures for the more exotic meson & baryon resonances. These structures could only be fitted to experimental mass-energy values by assuming that they were composed of larger numbers of smaller-spaced defect-pairs, rather than assuming that they had three huge-spaced defect-pairs in analogy to nucleons.
ഀ ഀThese larger numbers of defect-pairs could be fitted into the concept of three-axes particles, only by assuming that they were bound together by interior strong-force bonds. After years of fiddling, I was able to discover suitable bond spacings vs. bound defect-pair spacings that maintained a reasonable consistency over the entire group of resonances.
ഀ ഀThe application of these equations to nuclei involved guessing possible equilibrium spacings of inter-nuclear bonds, and then testing whether these spacings would yield the correct nuclear bond mass-deficit values. I did this repetitively on a liberal sample of low-A nuclei. This was too tedious a process to recount, but suffice to say, it eventually let me discover the range of typical nuclear bond spacings (8ü↔11ü), and let me learn a considerable amount about bond dynamics (I show a small sample of these tedious nuclear bond mass-deficit calculations in Chapter 3 of my online book). The fact that these average bond spacings are roughly equivalent to the defect-pair spacings of protons & neutrons is what leads to the regularity of nucleon arrangements in nuclear structures, as we shall soon see.
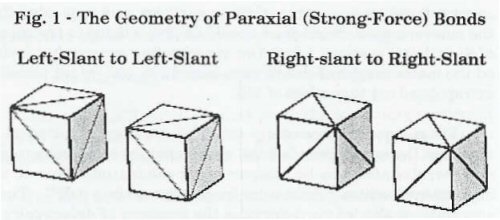
ഀ ഀ ഀBy a process of deduction from nuclear clues, particularly from the fact that 2He5 has an extremely short half-life, I have concluded that both protons and neutrons form with a T-slant arrangement of their three component defect-pairs. We visualize this as a condition whereby diagonal lines representing the axis of expansion on the six faces of of our nucleon "cube" are in a tetrahedral relationship. This deduction meets the criterion of parsimony, since there are only two T-slant forms, whereas, should we have chosen a "mixed-slant" alternative, we would find there are six permutations. Let us then identify the two T-slant forms as "right-slant" & "left-slant", depending upon whether the slant on the –x face intersects the +y,–z corner, or the +y,+z corner.
ഀ ഀ ഀIt should be clear, at this point, that the two c-voids of a defect-pair must have opposite "slants" for cancellation of E/C distortion to take place. And, this makes it quite clear that bonds between two co-linear defect-pairs in two nucleons spaced-apart on a common plane, must have the same slant forms, if their opposing c-voids are to have the required opposite slants for bonding. IPP calls this bonding configuration between two defect-pairs, a "paraxial bond". There are two equally probable slant relationships of paraxial bonds: left-slant to left slant, and right-slant to right-slant. I use the "cube" form of nucleons to show these slant relationships, below:
ഀ ഀ
If the planes of symmetry of two collapsed voids (of two defect-pairs) lie in the same cardinal plane of the lattice, we perceive that they could position themselves such that the axis of contraction of one lies in a lattice face-diagonal direction from the axis of expansion of the other (i.e., they possess opposite slants). In this configuration, their two residues of E/C distortion will partially cancel each other, and a bond will be established between them. In Fig. 2, below, I show the geometrical relationships between two nucleons (represented as T-slant cubes) that result in the formation of a diagonal bond between them:
ഀ ഀ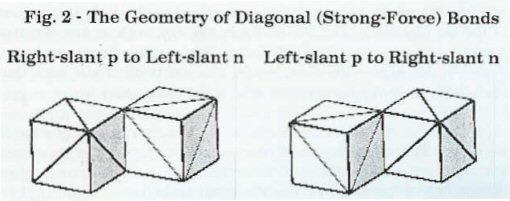
This combination of proton and neutron bound together with a diagonal bond is IPP's concept of a deuteride (1H2 nucleus). Since IPP assumes that both protons & neutrons occur in both T-slant forms, and that they bond together in either order, and in any of the six face-diagonal directions of the space lattice, we should see that these two structures, above, represent only two of twenty-four possible orientations & slant sequences in which a proton and neutron could form their diagonal bond in a specific crystal of polycrystalline space. We should presume that the initial bonding orientation is preserved as the deuteride's twelve c-voids translate through any particular space crystal, and that its absolute orientation changes only when it translates through a grain boundary into a space crystal of different cardinal orientation, or when it passes through a zone of "undedicated shrinkage" (temporarily unutilized shrinkage) sufficient to rupture its bond, thereby permitting its bond to form in perhaps a new orientation.
ഀ ഀDiagonal bonds are stable only between protons and neutrons, and this accounts for the fact that the stable isotopes of low-Z elements tend to have equal numbers of protons & neutrons. However, since the mutual cancellation of E/C distortion is indifferent to c-void charge, and neutrons don't repel each other, diagonal bonds can also form between suitably aligned neutrons, and can exist stably, provided the neutrons are sterically hindered from escaping from each other. This constrained situation occurs among neutrons that site in the interiors of larger clusters of nucleons, where neutrons gather together in all-neutron planes, as we shall see. Neutrons can also cluster together in modest numbers in the centers of single-plane nucleon clusters.
ഀ ഀ ഀUp to Z-numbers 20, I have deduced that protons and neutrons tend to cluster into a single plane that lies parallel to one of the three cardinal plane of the space lattice. These nucleons are bound together by a matrix of paraxial and diagonal bonds into an array that has the geometry of the black squares of a checkerboard.ഀ From Z=20 to Z=30, the nucleons cluster in single planes, except for their higher A-number stable isotopes & higher-A unstable isotopes, which appear to prefer the multi-plane form. I will not discuss the factors determining the geometry of single-plane structures in this article, but you can investigate them on my website if you are interested. I do show the single-plane structures of Titanium and a few other low-Z elements in my attempted explanation of the "Cincinnati Disclosure" nuclear transmutation result.
ഀ ഀFor Z-numbers above 24, I have concluded that some of the higher isotopes have single planes that extend over too large an area to survive passage through the grain boundaries of polycrystalline space (which passage requires that they bend progressively into a new cardinal orientation). We may imagine that the resulting breakup leads, in the normal solar environment, to smaller pieces that start over again in the buildup process. However, in the high-neutron flux of an exploding supernova, I infer that a much larger planar structure can be created before its breakup, and this group of pieces will form a core that will attract other nuclear debris, and rapidly self-organize into a multiple-plane configuration, bound together with inter-plane bonds. I have analysed this process in great depth on my website, particularly in Chapter 4 of the on-line book. When you read this analysis, you should see why I have come to the following rather astounding conclusion:
ഀ ഀMultiple-plane nucleon clusters can exist stably, only if they cluster into five, or seven parallel planes! Let's consider, first, the five-plane structures:
ഀ ഀPlanes 1,3,5 contain both protons and neutrons bound together by both paraxial & diagonal bonds in a checkerboard arrangement, much like single plane structures, only with fewer neutrons. For any element whose Z-number is divisible by three, the stable isotopes tend to have identical proton & neutron compositions and identical arrangements in these three planes (but there are exceptions). Protons will site above protons and neutrons will site above neutrons, and these nucleon stacks will be bound together with inter-plane paraxial bonds, whose bond spacings are in the 9ü↔11ü range.
ഀ ഀPlanes 2,4 contain only neutrons, which also are bound together by both paraxial & diagonal bonds in checkerboard arrays, but the two planes contain variable amounts of neutrons, depending upon the particular A-number of an element's isotope. The neutrons in these two all-neutron planes are also bound together with inter-plane paraxial bonds, and this requires that these neutron planes be offset relative to the 1,3,5 planes.
ഀ ഀAs you might imagine, bonding between adjacent planes is critical to the stability of five-plane nuclear structures. Upon initial reflection, this would seem to be no problem, since almost every nucleon in each plane is bound to a nucleon two planes away with a paraxial bond. Well, there would be no problem if paraxial bonds were unconditionally stable, but experiments tell us that di-protons and di-neutrons have very short mean lifetimes, which suggests that a single lattice-unit of lateral displacement of the paired c-void centers ruptures a paraxial bond. We infer, then, that multiplane nuclei could not survive the severe bending action of grain-boundary passage, if there were not some other bonds between planes preventing this lateral slippage. There are, and this is the function of the diagonal bonds that form between adjacent planes.
ഀ ഀSince adjacent planes must be offset for paraxial bonds to tie like-type planes together, as I have already explained, we perceive that only diagonal bonds are possible between adjacent planes, and these bonds are less sensitive to misalignment, since the E/C cancellations merely diminish, rather than extinguish, when diagonal bonding c-voids centers are displaced from optimum face-diagonal alignment. But these diagonal bonds bring with them another problem; they can be repulsive as well as attractive, and, in fact, throughout the bulk of the inter-plane contacts, there are equal numbers of each type.
ഀ ഀIt is only at the perimeter of the five planes that attractive diagonal bonds exceed repulsive ones, and these are only on two of the four sides (of the usual rectangular cluster form). The geometry required is that an "edge" neutron of plane 2, or 4, sites above or beneath a dual-proton "notch", and that this edge-neutron is the opposite slant-type from the two edge-protons constituting this "notch". In this spot the plane 2/4 "edge" neutron develops two attractive diagonal bonds with the two protons, and one repulsive bond with the plane 1/3/5 neutron in the second row. This yields a net bond of one attractive diagonal bond between it and each contiguous plane.
ഀ ഀAt least four of these attractive "notch" bonds for each 1/3/5 plane are necessary for a nuclide to be stable. If you keep this requirement in mind, you will begin to understand the reason that protons prefer to gather into rectangular, rather than diamond shape, arrays (this permits more notch bonds), and you will perceive the importance of nearly saturated 2/4 plane neutron "rafts" for nuclide stability (this increases the number of 2/4 "notch" neutrons).
ഀ ഀYou will notice in the following nuclide structures that the orthogonal dual-proton "notches" are normally unoccupied. These are avoided by plane 2/4 neutrons because a neutron siting in these orthogonal dual-proton "notches" would develop two repulsive db's and only one attractive db, because this neutron's T-slant form would be the same as the two proton's. You will perhaps see, however, that these "notches" can become the dominant interplane bonding locations simply by reversal of all the "slants" of all the 2/4 plane neutrons. There is good evidence that this sometimes occurs among elements whose proton placements assume a completely-filled rectangular form. The clue for this binding direction shift is the presence of two nearly equally abundant stable isotopes that are four A-numbers apart.
ഀ ഀIt has taken me three decades to sift through all the arguments and evidence needed to reach the above conclusions, and it could take months of intense study on your part to become convinced that these conclusions are justified. But I hope that you have understood enough to appreciate the nuances of the structures that come next.
ഀ ഀ ഀThe group of schematics, that follow, are designed to show the specific planar locations of all the component protons and neutrons of the various five-plane nuclides that are involved in my LENR investigations #2, #3, & #4. What makes a simple depiction of these three-dimensional structures possible is that neutrons of planes 2/4 site under the "holes" in the 1/3/5 planes, and that the protons and neutrons of planes 1/3/5 stack above nucleons of the same type, i.e., protons above protons & neutrons above neutrons. Compelling evidence for this last assertion is found in elements whose Z÷3 yields a factorable residue, like 90÷3=6x5; 75÷3=5x5; 60÷3=5x4. I will show you the structures of these three nuclides as my first exhibit, just as soon as I show you how to read the schematics that let you perceive their three-dimensional structures.
ഀ ഀThe geometrical relationships that prevail between the nucleons of the five planes permit us to represent the exact location of all the nucleons in a five-plane cluster of nucleon with a single plane of appropriate symbols. These symbols are of two types: one group represents the nucleons in either one, two, or all of the three planes, 1/3/5, which, as I have already explained, are composed of diagonally alternating protons & neutrons, much like single-plane nuclide structures. A second set of symbols is designed to show the locations of neutrons in either, or both, of the two all-neutron planes, 2/4. These are chevron symbols which have an additional function, that of showing the specific T-slant direction of each neutron in these two planes. With this 2/4 slant information you will be able to infer the slant directions of the protons and neutrons in planes 1/3/5. It is only necessary to remember that the slant of the "notch" neutrons of planes 2/4 are required to be opposite to the slant of the "notch" protons of planes 1/3/5.
ഀ ഀ

If you are sharp, you will notice that the "alpha sidewise view" is not a valid representation of the alpha two state charge-exchange, because it shows the center shifting downward from plane 3 level to plane 2 level, whereas it should remain on the same level for both states. But, actually, this is immaterial, since the alpha structure never occurs within five-plane nuclear structures; it adopts its two-state charge-exchange cycle only as it emerges in alpha emission. But it does exist as peripheral groups in single-plane nuclei, as I show for carbon 12 & carbon 13, above. Notice that 6C13's extra neutron must site asymmetrically; hence its negative spin parity. Also notice that adding a neutron to 6C13, in the upper left spot, produces a bilaterally symmetrical structure, justifying a 0+ spin for 6C14.
ഀ ഀNow let us shift from small nuclei to very large ones. Here are four examples of "completely saturated" structures that I promised to show you:
ഀ ഀ
Note: the sums below the diagrams are the way I keep track of the component nucleon counts. The first line is the total count of 1/3/5 protons = Z; the second line is the count of 1/3/5 neutrons; the third line is the count of 2/4 neutrons; the fourth line is the total number of nucleons = A. Also, note the shift of the "notch" neutron bonding locations from four-notch to three-notch sides in the two neodymium "saturated" structures.
ഀ ഀWe should now have enough insights into IPP's concepts to begin the last three investigations I listed at the beginning of this document. We shall begin with investigation #2, in which I shall endeavor to explain the nuclear reactions that result in the production of helium in "cold-fusion" experiments.
ഀ ഀ ഀ ഀ ഀ ഀ ഀ******************************************************
ഀ ഀI think you will agree that the fundamental problem to solve in LENR is this:
ഀ ഀHow does D (or H) get to the nuclide surface?
ഀ ഀWe all accept that these hydrogen isotopes arrive at the palladium cathode surface as positive ions, but what happens at this liquid-solid interface, teeming with free electrons, that lets these positive charge ions penetrate through this electron cloud, and through the forty-six electrons that surround each nucleus, and then arrive at the nuclide surface, despite the very strong retarding field of the nuclear positive charge? It would seem that only a neutral particle could get through these changing fields unimpeded, and this calls to mind the hydrino concept of Dr. Randell Mills Theory. Perhaps the following is a credible scenario:
ഀ ഀLet's begin by considering the geometry of the perimeter sites that would let a palladium nuclide capture a deuteride and evolve an alpha particle. Now that you are aware of the meaning of IPP's nuclear symbols, I can show you what these two sites should look like:
ഀ ഀ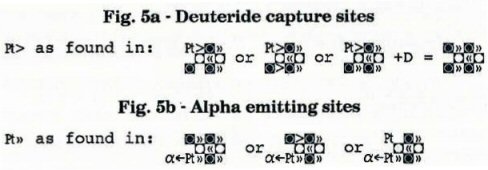
We will not find both of these sites in a stable nuclide. Many stable nuclides have deuteride capture sites, as I show above, but the alpha emitting structure has a poorly bound plane 4 neutron, which sooner or later decays by ß- emission into a proton, which then moves into a proton location. This difficulty complicates the problem of finding a nuclide that satisfies our desiderata, because we must find one that undergoes an internal transition upon capturing a deuteride, and not just any internal transition, but one that is sure to move a neutron into this plane 4 corner location.
ഀ ഀLet us see if we can discover the structural feature below in Fig. 6a that would induce neutron movement, when a D bonds. A clue staring us in the face is the different look of the one odd-n isotope, 46Pd105, compared to the three even-n isotopes. It has only three neutron three-stacks in the central row vs. four for the even. Then looking closer we see that it has two more 2/4 neutrons in the second column, than does 46Pd106 to its right. Ah-ha!, we say, neutrons move back and forth between the central row and the second column as the number of neutrons, A-Z, changes from even to odd:
ഀ ഀ
The relevance of our observation about neutron movement between even-n & odd-n isotopes is that when a deuteride adds to an even-n palladium isotope it changes it into an odd-n isotope of silver. Thus, we will expect the three neutrons in the right three-stack in the central row to move into the second column, and to add to however many neutrons are already there. This makes it easy for us to chose a palladium isotope that fulfills our requirements for alpha emission --- we need only look for an even isotope that already has four (or more) neutrons in the second column before the deuteride adds. Looking at the structures directly above, we see that both 46Pd108 & 46Pd110 satisfy this requirement. Let us look at these before and after D bonds to them:
ഀ ഀ
When the D adds to the upper left-hand proton two-stack, and the resulting excited state induces an immediate internal transition, we may expect that greater bonding now accrues to the plane 4 locations in column 2, than in the right-hand three-stack of the central row. This causes the 1/3/5 neutrons of the central row to move into these vacant plane 4 locations of column 2 by a process I call a "bucket-brigade". We can imagine the process something like this:ഀ Let's look at 46Pd108 to describe this "bucket-brigade" process.
ഀ ഀ
At this stage of my investigation of alpha emission from palladium, you have every right to ask the embarrassing question, "If the experimental data about 47Ag110 & 47Ag112 make no mention of alpha emission, why should making these by deuteride addition cause alpha emission to happen?". I can answer this question in two ways, superficially, and deeply, with much rather boring analysis.
ഀ ഀThe superficial answer is that the bonding mass-deficit of the deuteride attachment places the resulting silver isotope in an excited state, and this causes various bonds in this structure to increase their bond spacings, thereby reducing the added amount of externally supplied mass-energy (shrinkage) necessary to rupture them. If this stretching occurs in the bonds that attach the 2p2n group to the nuclide, there is a possibility that this group can separate far enough so that it can rearrange into an alpha particle. This rearrangement results in a rather large release of mass-energy, and this extra increment may be sufficient to break any residual bonds, and free the alpha particle.
ഀ ഀThe superficial analysis, in this case, leaves us unsatisfied, because we have learned nothing that tells us whether or not alpha emission will occur. To get more insight, we need to make a bond count of the new bonds that are formed by the deuteride's capture, and compare these with the count of the bonds that must be broken to free the 2p2n group. I take up this problem next:
ഀ ഀWe have learned enough about paraxial and diagonal bonds that we shall have no difficulty counting the bonds mentioned above that tie these groups to the nuclide body. The definitive approach would be to convert each bond to a mass-deficit value, sum these values, and then make comparisons. But my understanding of bond calculations in large nuclei is not sufficient for this to be possible. So we shall take the fallback option of considering that paraxial & diagonal bonds in various nuclear locations are sufficiently close in bond mass-deficit values that we can form useful conclusions just by comparing the numbers of bonds of similar types.
ഀ ഀWhat seems necessary, in view of the migration of neutrons brought on by the induced internal transition, is to count the bonds of these two groups, the deuteride, and the 2p2n group, after the rearrangement has taken place, i.e., as in the structure, 47Ag110, in Fig. 7. Here are the final numbers, broken down into three categories, pb's (paraxial bonds), db's (diagonal bonds), and nb's ("notch" bonds, which are diagonal bonds between planes). Notice that these bond counts are made individually for protons & neutrons:
ഀ ഀ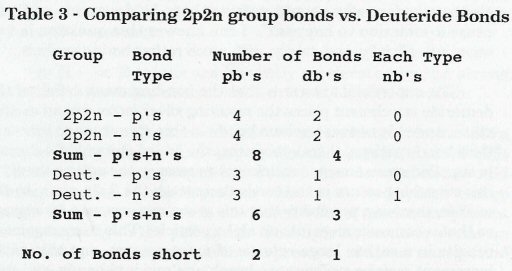
Note: If you are wondering why no "notch" bonds are listed in the 2p2n tally, notice that the notch bonds that need to be broken have equal numbers of attractive and repulsive bonds, so they cancel each other. The other attractive bonds, that yielded the one net diagonal bond per plane, leave with the 2p2n group.
ഀ ഀ ഀArgument from Above Data
ഀ ഀWhat we conclude is that the mass-energy released by the above process is inadequate to break the bonds that hold the corner 2p/2n group in place. For this 2p/2n group to be released, an additional mass-energy equivalent to 2pb+1db has to be supplied. However, we are not through with our analysis. If we recall that the bonding mass-deficit of an alpha particle is –28.30 MeV, we should see that more than enough mass-energy is available to free the 2p/2n group, provided it can get far enough away from the nuclide body to allow the a-rearrangement into its two-state charge-exchange cycle to take place. This is the usual quantum paradox: the 2p/2n group needs to be released in order to be released!
ഀ ഀFortunately, IPP has developed two new tools that let us resolve this paradox. The first tool has to do with IPP's ability to show the components of the alpha particle's binding mass-deficit. The definitive way for you to find this out is to go to page 18, Chapter 3, of the online book, where the whole process of the two-state charge-exchange is drawn in 3-D and dissected in every detail. But, perhaps just showing you the significant details will serve our purpose:
ഀ ഀArgument:
ഀ ഀIf the mass-deficit of alpha's 2pb,4db bonds = –12.81 MeV, then the additional mass-energy (equivalent to 2pb,1db) required to free the 2p/2n group from the nuclide should be about half that amount ≈ +6.4 MeV. This can easily be supplied from the +15.47 MeV released when the four nucleons switch from six-state to two-state charge exchange cycles, and thus the 2p/2n group has enough mass-energy available to shake it free, if it can get free. We take up this question next:
ഀ ഀ ഀBut how does this 2p2n group shake free before this mass-energy is supplied by its rearrangement into an alpha? Here is where IPP's second new tool is brought into play. This is the notion that space is polycrystalline. If you require any justification for this notion, try to imagine any process that fills space completely with ECEs to the boundaries of our observed universe in a manner that is so free from turbulence that it leaves the whole universe in the form of a single crystal. You can't! The only thing, then, that is worth thinking about is, "What size are the crystals of polycrystalline space?"
ഀ ഀThere is much room for speculation. ECEs are very small; there are about 750 inside the "cube" of a proton or neutron, about a billion-billion within the chemist's boundary of a hydrogen atom, and about 1.25e41 inside a cubic centimeter. This tells us that space crystals could be absolutely huge in relation to the number of ECE contained in them, and yet be exceedingly tiny, perhaps so tiny that a nucleus might pass through millions of them per centimeter of travel. Or they might be so huge that a nucleus might pass through only a thousand per centimeter of travel. Or pick any size that pleases you more, or think of some experiment that might allow us to determine their average size.
ഀ ഀWhat is relevant to our problem of getting an alpha particle emitted from a nucleus is the probability that a nucleus will be passing through countless grain boundaries in the time duration of a typical nuclear reaction. Each passage of a nucleus through a grain boundary imposes a burden upon all their component nucleons to alter the absolute orientations of their three mutually orthogonal defect-pairs such that they now align with the new cardinal directions of this new space crystal. If we think of the structure of a large nuclide, we will perceive these changes as progressing in a wave-like motion of bond-breaking and rebonding, moving from the part first to enter the grain boundary to the part last to enter.
ഀ ഀThe degree of difficulty in executing this warping motion clearly depends upon the geometry of the encounter. We can ask many questions: What is angle of trajectory of the nuclide relative to the plane of the grain boundary? What is the nuclide's orientation relative to the grain-boundary plane? Does the warping occur in the length, width, or thickness direction? Does the grain boundary have a simple plane configuration, or is it convoluted in steps, pyramids, or spiral dislocations?
ഀ ഀAll of these variations are relevant to our discerning the effect of passage through the grain boundary upon the α–emitting corner of our current interest. What perhaps we can say is whatever we imagine as the precise orientation relative to the grain boundary that we feel is necessary for sufficient separation of our 2p2n group from the nuclide body to create the alpha particle, sooner or later it will occur. It might take hundreds, or millions, or trillions of rotations & tumblings to arrive at the exact geometry needed, but if it can happen, it will!
ഀ ഀWhat seems necessary, to me, to induce the alpha particle generating process is for the nuclide corner of interest to be the last to enter the grain boundary, and to enter it diagonally, and perhaps for there to be a specific timing of this passage relative to the synchronized six-state charge-exchanges of the 2p2n group. (There are good reasons to believe that all of a nuclide's charge-exchanges are synchronized). These conditions could result in sufficient nucleon jumbling and separation to permit the 2p/2n group to rearrange into an alpha configuration, whose +15.47 MeV release of mass-energy is used in two ways. About +6.5 MeV is accepted by the nuclide residue, 45Rh106, in payment for the 2pb,1db bond deficit it suffered when the 2p2n group left, and the remaining approx. 9.0 MeV of undedicated shrinkage splits into two equal pieces that attach to the two closest ECE packing-density oscillators, the alpha's and the nuclide's to alter their respective ellipticities such that they separate from each other. This increased motion is interpreted by the experimenter as excess heat.
ഀ ഀ ഀAlthough our immediate concern is the effect of countless grain-boundary encounters upon nuclei, perhaps we should take a moment to broaden our enquiry to include the effects of grain boundary transits upon photons and leptons. Compared with nuclei, these are very simple structures, the photons being pure, but very elongated ellipsoidal ECE packing density oscillations, and the leptons being ellipsoidal oscillations of all degrees of ellipticity (depending upon their drift velocities), with one, or two central defects, whose distortion effects don't deviate much from spherical symmetry.
ഀ ഀIt should also be clear that ECE packing-density oscillations are infinitely larger than any plausible grain-boundary size, and that their mass-energy is distributed in equal radial increments to infinity. This makes them essentially immune to the constant grain-boundary deflections that their centers are subject to, because so little of their total mass-energy is in their centers. These deflections simply integrate out to nothing.
ഀ ഀWhat accounts for Heisenberg's "uncertainty" in IPP theory is not grain boundary encounters, but the presence in the space lattice of countless lattice voids, perhaps billions of times more numerous than hadron particles. Lone voids (muon neutrinos) possess charges of ±1/2e, and at thermal velocities in free space have so little mass-energy that they are completely undetectable. However, they have one other outstanding property --- they can become quite massive in the presence of undedicated shrinkage by collapsing into a c-void. So when they wander into the vicinity of nuclei they can momentarily capture the shrinkage that is released during the low mass-energy states of a nuclide's six-state charge-exchange cycle, and get massive enough to cause substantial deflection of close-by particles.
ഀ ഀHere is an obvious source of "uncertainty", i.e., things we can't detect deflecting things we can. Voids are so abundant, and so inconsequential, that they permeate everything without leaving any obvious traces. Notice how easily we can understand the baffling phenomenon of "tunneling", if we assume that the distribution of voids is purely random. Randomness suggests that there must occasionally be large local excesses of either polarity of voids, and a local excess of positive voids, collapsed by being close to local semiconductor nuclei, could easily gate local electrons through a reverse-biased junction.
ഀ ഀA parting comment: Up to this point, for pedagogical conciseness, I have used my authoritative voice, with few temporizing statements. This approach is bound create a false impression that "all is placid and perfect in my art", but this is far from true! I feel relatively pleased with my choices, but I am not married to them. I have made thousands of nuclear structural diagrams, but I need to make thousands more to feel even reasonably secure. One of the aspects of the "cold fusion" phenomena that I find tremendously exciting is that it offers the prospect of testing my nuclear structural ideas in the experimental arena. If tests can be made with separated isotopes of palladium, and other elements mentioned in this paper, and the predicted differences are found (or not found) in their "cold fusion" behavior, then we should be able gradually to learn what aspects of these nuclear structures are crucial to this process.
ഀ ഀ ഀ ഀ ഀ ഀ ഀ ഀ ഀ ഀ ഀ******************************************************
ഀ ഀIn Issue 52, 2003 of INFINITE ENERGY, page 10, there is a note that A. Takahashi group at Osaka University has reconfirmed the earlier findings of the Mitsubishi Industries Advanced Technology Division of nuclear transmutations, Cs → Pr and Sr → Mo, just by flowing deuterium gas through a palladium membrane onto which either cesium or strontium has been deposited. I show below the changing nuclear structures that illustrate this chain of nuclear transmutations:
ഀ ഀ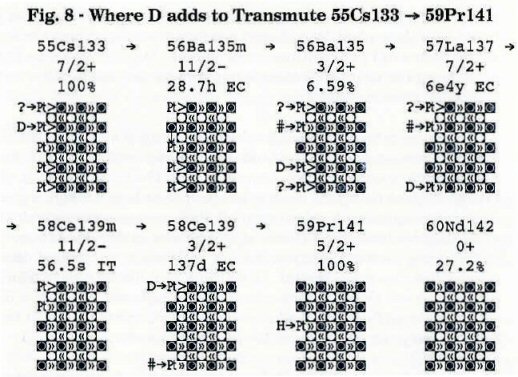
I indicate, above, where I expect the deuteride (D→) to add to each of the above nuclides. I use the question mark (?→) to indicate another addition point that seems initially to have nearly equal plausibility, but if you look carefully you will see that the questionable sites always develop fewer bonds. The mark (#→) indicates a place where deuterium can't add, because there is no adjacent vacancy in plane 4 to accept the deuteride's neutron. In the deuterium addition (D→) to Cs, I have indicated that the deuteride proton bonds initially in the third row to produce 34Ba135m (an IT state), but I have presumed that the internal transition to 34Ba135 (6.592%) occurs immediately, rather than with the measured half-life of 28.7 hours, because the capture of the deuteride puts the nuclide in an excited state. Perhaps my presumption of this immediate shift of a proton to the central row to gain additional nuclide pairing could be determined by the presence, or absence, of 0.268 MeV gammas in the wealth of gamma radiation that this whole sequence of nuclear transmutations is certain to release. A similar study could look for the presence, or absence, of 0.754 MeV gammas in the internal transition of 36Ce139m → 36Ce139.
ഀ ഀNote: The only possibility of alpha emission, in this sequence of deuteride induced transmutations, is in the structure I show for 58Ce139. This is the only one of this group of structures that exhibits the required weakly-bonded corner group of 2p,2n. However, if this structure invariably resulted in alpha emission, the transmutation sequence would never end, but would recycle endlessly between 56Ba135 → 57La137 → 58Ce139 → 56Ba135 → 57La137 etc., etc. If this were what happens, then barium deposited upon palladium would obviously be an ideal nuclear energy source, since the two elements would never be used up, but would simply function as catalysts that convert 1H2 to energy plus 2He4. However, since the transmutation sequence ends in praseodymium, rather than barium, we must temper our enthusiasm, and infer, instead, that one of these four alternatives is true:
ഀ ഀThe Fig. 8 structure of praseodymium makes it obvious why 59Pr141 is unable to capture a D: There is no suitable bonding location for the deuteride neutron, because the plane 4, 2nd column, row 5 neutron location is already filled. There is, however, a strong bonding site for a proton, which would produce 60Nd140, but this addition doesn't seem to happen. What prevents this? Here is a puzzle, because even the purest deuterium gas will inevitably have light hydrogen mixed with it. So what keeps these protons from bonding to 59Pr141?
ഀ ഀOne answer has to do with the different electron energy levels that exist beneath the ground states of hydrogen vs. deuterium in the Randell Mills "black-light" process. If my suggestion is valid that stable neutral hydrinos are the means by which both hydrogen and deuterium can actually reach the nuclide surface to bond with it, then an impurity element in palladium must have excited states that are properly "tuned" only to the quantized outpourings of the deuteride atom, as its electron drops down to the hydrino level. We should not be surprised, then, if this essential impurity that catalyses deuterium collapse fails to work with hydrogen.
ഀ ഀExperimenters could perhaps test the hydrino hypothesis by adding larger amounts of each palladium impurity, in turn, and measuring the rate of reactions, and excess energy formation for each impurity. Having validated the impurity hypothesis, they could then add potassium (or other proven catalyst elements used in the Mills experiments) to see if the transmutation series ends with neodymium, rather than with praseodymium.
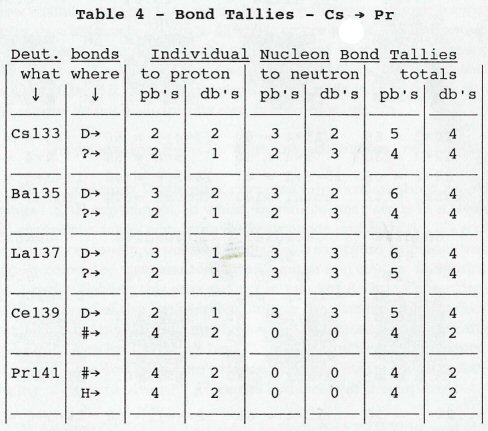
ഀ ഀI'm certain that many of you won't need to study Table 4, below, to be assured that I have chosen the most appropriate deuteride addition locations in the nuclear transmutation series of Fig. 9. However, in deference to readers whose minds prefer their decisions to be based upon quantitative data, I have compiled the bond tallies for both the D→ addition, and for the ?→ addition. You will note that the total bond count of D→ exceeds that of ?→ for each nuclide. Thus we may presume that the mass-deficits of the D→ additions exceed those of the ?→ additions, and will, therefore, be the deuteride attachment points for the transmutations shown.
ഀ ഀ
In the last row of the table, I show that a proton addition (H→) to 59Pr141 is very strongly bonded, and would lead to 60Nd142, a completely "saturated" structure. However, an even larger "saturated" structure of neodymium can form if it acquires four more 2/4 neutrons (two of each slant type). This larger group of 2/4 neutrons can fit into another completely "saturated" structure, 60Nd146 (17.2%), if they arrange themselves such that their "notch" neutrons are bound on the four-proton-notch sides.
ഀ ഀYou will recall that these two Neodymium structures were among the four "completely saturated" nuclides that I presented as Fig. 3. This switch in the location of the "notch" neutrons is not the only interesting aspect of neodymium. All the rest of its stable isotopes are seven-plane structures, and these seven-plane isotopes also show a wealth of structural variations among themselves as A-numbers increase and alternate between even and odd:
ഀ ഀ ഀ

I hope you will take the time to look closely at these neodymium structures, for they convey some important insights into the structural aspects of nuclear stability and of nuclear decay that will be useful in perceiving why LENR occur.
ഀ ഀThree of the above structures are particularly instructive: 60Nd144, 60Nd147, & 60Nd150. These isotopes are observed to decay in different modes (144 → α; 147 → ß–; 150 → 2ß–), yet these decay differences are not evident in the structures shown. In fact, none even has any of the features that we commonly associate with these decays! Fortunately, IPP's tool of "energy exchanges in grain-boundary transits" lets us imagine alternative structures of lesser bond mass-deficits that have the appropriate decay structures. You may visualize my concept of these decay-promoting structures by replacing the right two columns of each of these three structures by the isolated two columns further right.
ഀ ഀIf you examine these two structural options for each isotope, you will see that, in the "decay" structure, the weakest bonded nucleon is attached with fewer strong-force bonds than it is in the "stable" structure. This insight, less bonds = less stability, is obvious, but, also, of limited usefulness, since the number of bonds required for stability is a function of nuclide size and shape.
ഀ ഀThe notion of "stable" & "unstable" structural options raises two interesting questions: What causes the more strongly bonded form to change into the lesser bonded form? What is the source of mass-energy that must be added to effect this change?
ഀ ഀIPP would say that both the cause of the shifting nucleon and the energy source that permits it to happen derive from an atypical passage through a lattice grain-boundary. In a nuclide's transit through a succession of grain boundaries, strong-force bonds will be stretched or broken progressively throughout the entire nuclide structure. This disruption sets in motion a progressive process of new bond formation, which almost always recapitulates the previous structure, but there is always a possibility of creating a structural variation that persists, if the passage also results in a change in the geometry of the grain boundary.
ഀ ഀWhat we should imagine is that grain-boundaries may have regions of convoluted geometry that capture more shrinkage per unit area than smoother regions, and that some of this mass-energy may be released if a nuclide's passage causes this region to rearrange into a less complex geometry. As usual, in these energy interchanges, the nuclide can capture only half of the released energy, the other half spawning an oppositely-directed photon. And, of course, the nuclide captured energy divides between supporting quantized bond spacing increases and increasing nuclide momentum. Also, for these processes to go on through infinite time, we must allow the reverse scenario, in which the nuclide's passage convolutes a smoother grain-boundary area, causing mass-energy absorption, which decreases the nuclide's momentum, and/or reverts its structure to its ground state, or induces a particle releasing decay mode.
ഀ ഀNow, with this complicated analysis under our belts, we can take a simplified approach to the second group of "Mitsubishi Modern Alchemy" transmutations:
ഀ ഀ ഀI will assume for this demonstration that you have studied the Cs → Pr example, for I shall not make a tally of bonds to justify my choice of where the deuteride adds. I think you will perceive that adding to either of the left column proton two-stacks will yield one more proton and one more neutron paraxial bond (because of the proton three-stack, and 2/4 neutron two-stack, midway between them) than adding to the right column two stacks, where these nucleons are missing. Also, I'm sure that you see that deuteride addition must stop when 42Mo94 is formed, because there is no suitable bonding site present on that structure for the D neutron. A proton could add in the location indicated by "←H", but this has the same difficulty (lack of a suitable hydrino H-catalyst) as adding a proton to 59Pr141, and the same remedy (provide one).
ഀ ഀ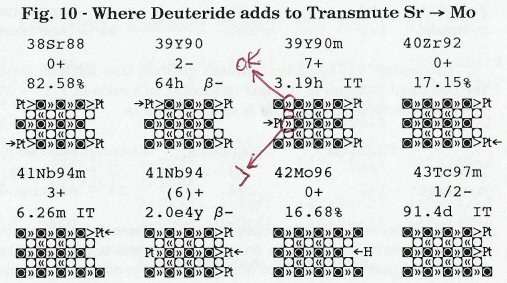
I indicate, above, with a simple arrow (→ or ←) where I expect the deuteride to add to each of the above nuclides. These additions follow a similar pattern to those in the Cs → Pr series, except for the deuteride additions to 39Y90 & 41Nb94, where an internal transition is encountered, which causes the addition point to change. Actually, addition at either of these two points will yield the same structures for both 40Zr92 & 42Mo96, because, as we have learned, each isotope churns its nucleons into its own preferred structure.
ഀ ഀ ഀ ഀ ഀ ഀ ഀ ഀ ഀ ഀ ഀ ഀ******************************************************
ഀ ഀThe "Cincinnati Disclosure" revealed information about a very curious LENR experiment, in which, by simple electrolysis in a weak acid electrolyte, using zirconium for both anode and cathode, 0.1 g of thorium, previously deposited upon the zirconium cathode, was entirely converted (transmuted) into titanium and copper, in approx. a 10:1 ratio. Solving this case put me in mind of Arthur Conan Doyle's "The Hound of the Baskervilles", where the clue that let Sherlock Holmes crack this baffling mystery was the absence of something expected: "The hound didn't bark!” In the Cincinnati Disclosure, the crucial clue is: "Why didn't the experimenters find a huge outpouring of extra neutrons?” Here are two facets of this mystery:
ഀ ഀ

One interesting thing we can infer from these data is that there are enough neutrons left over in both examples to create 29Cu63, if we could just find a way to bring 27 or 26 protons to thorium's perimeter, and get them to bond to it. And not just to bond, but, to attach in such a gentle manner that successive additions do not strip off those already attached, until all the 27 (26) arriving protons have established their bonds.
ഀ ഀIs this LENR scenario possible? A gentle arrival seems assured, if we subscribe to the notion that electrolysis produces a flood of slowly drifting, neutral hydrinos that can intersect any nuclei in their drift paths. We should even expect a feeble attraction that will deflect the drift paths toward the nucleus, due to dipole rotation of electron & proton components of the neutral particle. But, what about gentle bonding; what could lead to this?
ഀ ഀLet's look at Fig. 11, and do a little exploring around the proton-rich perimeter of 90Th232's perfect five-plane structure, to see where a proton can bond. It is perfectly obvious that there are no edge-bonding locations in planes 1/3/5, because all we see in these planes are dual-proton notches, and we have accepted that protons can't form attractive diagonal bonds with protons, only with neutrons. But, we do see eight dual-neutron notches in planes 2/4 among the ten "notch-neutrons" on each of the longer sides of this rectangular structure. Each of these dual-neutron notches can bond an exterior proton with two attractive diagonal bonds, provided that its slant form is opposite to the neutrons' slants. However, each of these sites also forms two repulsive diagonal bonds with dual proton notches that exist between planes 1 & 3, or planes 3 & 5. The result: no net diagonal bonding in any of these sites.
ഀ ഀBut we have overlooked one other bond possibility: there are neutrons in the next row inward from the surface, which have the same slant as the attaching proton, and with which the proton can form an attractive paraxial bond. This seems to create a bonding situation that meets our requirement for "gentleness" --- just one bond holds each proton to the exterior of the thorium structure!
ഀ ഀIf we look at the "Surface Bonds" diagram, we find the identical bonding conditions, i.e., two attracting, two repelling diagonal bonds, and one attractive paraxial bond to a plane 4 (or plane 2) neutron of the same slant as the proton:
ഀ ഀ
So, we see that there are 48 weak surface-bonding locations for protons on the thorium nuclide. But is it reasonable to think that protons can move into bonding locations on planes that are dominated by positive-charge nucleons? To understand why this can happen, we need to use another of IPP's intellectual tools, "charge-exchanges". Here are some significant details about them:
ഀ ഀ
I show various ways that thorium with various numbers of attached protons can fractionate into titanium and copper in Table 6. The heading, "n's l.o.", means "neutrons left over" (i.e., the residue of 90Th232's neutrons that weren't utilized in forming the indicated isotopes). Only #5 → #8 would result in no emitted neutrons, although #1 → #4 could form without detected neutrons, if arriving neutral hydrinos combine with them to form deuterium.
ഀ ഀ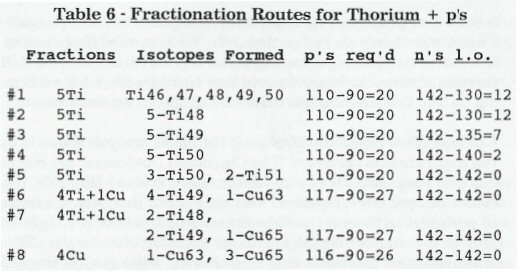
Let's look at the details of the above eight possible fractionation routes, to try to decide which are more likely to occur. Here's what comes to my mind as I look at these details:
ഀ ഀConclusions: About the only thing the above analysis shows is that the experimental results of "The Cincinnati Disclosure" are consistent with some mixture of some of the above routes. However, these routes at least show a process that can reduce the ratio of neutrons to protons in a thorium nuclide cluster sufficient for it to split into four or five smaller nuclides without emission of neutrons. These scenarios also give us a way of picturing what may actually be happening at the microcosmic level in these strange low-energy nuclear transmutations. Perhaps suitable experiments can be devised that will show whether or not hydrogen hydrinos are produced, and whether they can bond in multiple numbers to the surfaces of large nuclides, and whether they have the capability of combining with the few neutrons released in some of these low-energy nuclear fissions to produce deuterides.
ഀ ഀ ഀWhat is interesting about the structure of thorium's nuclide is that its 30 proton three-stacks divide neatly into five equal groups of 2x3 three-stacks (18 protons each), as I show below in the middle schematic. What is even more interesting is what happens if this breakup is caused by the surface attachment of 20 drifting hydrinos, in the locations shown in the left schematic. We see that these 20 protons are attached in locations that cause 4 extra protons to leave with each separating group, making 22 protons each. Here is a plausible way for 90Th232 to fractionate into 5 titanium nuclides:
ഀ ഀ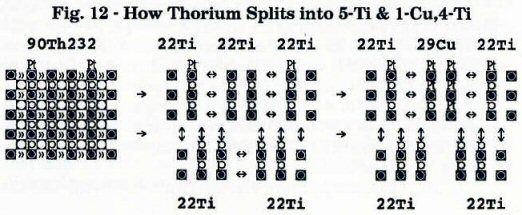
In the right-hand schematic I show a possible way for the top middle group to add sufficient extra protons to separate as a copper nuclide. To understand the geometry of this arrangement, you will need to give a new interpretation of the symbol, “P”, in the top three surface "hole" locations as meaning protons siting in planes #0 and planes #6. This scenario seems to me to be the most plausible way for thorium to split into copper plus four titanium isotopes although there are still quite a few mysteries. Among these are:
ഀ ഀIf we imagine that the above two modes of splitting of 90Th232 have nearly equal probability of occurring, we would expect 9 titanium nuclides for each copper nuclide, which is close to the 10/1 ratio that has been reported in the Cincinnati Disclosure.
ഀ ഀ ഀAs I mentioned in the Abstract of Investigation #4, the nuclei that result from the electrolytic fractionation of 90Th232 lie in the intermediate region between single plane and multiple plane structures. Thus, it behooves us to look at both structural possibilities for the various titanium isotopes that were detected in the end products of electrolysis, to see if we can find a reason or an argument to prefer one structural mode to the other. I take up the reason first:
ഀ ഀA reason to prefer the single-plane option is that we seek some source of mass-energy sufficient to break the bonds that join the five 18-proton groups to each other. We see that rearrangement into a single plane structure could possibly supply this needed mass-energy, if its binding mass-deficit were substantially greater than that of the five-plane form. We can imagine the breaking-off process as a king-size analog to the alpha emission scenario, which, you will recall, I discussed in Investigation #2. Here, we presume that a grain boundary transit initiates sufficient group separation through bond stretching to enable multiple-plane-to-single-plane rearrangements, whose released mass-energy makes the separation permanent.
ഀ ഀBut will the nucleons of the split-off group adopt the single-plane form? If we could make an accurate bond mass-deficit calculation for any conceivable structure, it would be easy to decide, but we're not able to do this yet. For now, then, we must choose between the two possibilities by seeing how well each structural type explains the way the experimental data varies with changing A-numbers. I find two criteria most helpful: 1) whether the most abundant isotope manifests the greatest symmetry among all the stable isotopes, and 2) whether the odd-n isotopes have structural asymmetries that are consistent with their measured nuclear spins. The single-plane forms for titanium appear to satisfy both of these criteria, as the schematics below show, whereas the five-plane forms fail in both regards.
ഀ ഀ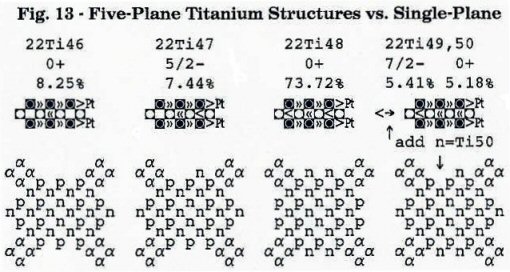
There are two reasons why we should expect the single plane forms to have substantially more bond mass-deficits: 1) they have substantially more "interior" nucleons (which have 4pb & 4db), and 2) they have four "outrigger" alpha groups with two-state charge-exchange cycles (each requiring –15.47 MeV less captured mass-energy to form its 2 protons & 2 neutrons). We can infer that these alpha groups exist, from the large increments of neutron separation energies that occur stepwise in the unstable isotopes immediately preceding the group of stable isotopes. Alpha groups can form only at the periphery of the nuclide core, because their y-defect-pairs shift sidewise back-and-forth each charge-exchange, and this action can be mirrored only in a limited way by nucleons that are in the six-state charge-exchange. See online book for further details.
ഀ ഀWe will use the same criteria to answer this question, as we used for titanium, but in this case we come to the opposite conclusion. If we look at the schematics below, we see that only the five-plane structures have the asymmetry that we can associate with negative parity. Also we see that Cu63, the more abundant isotope, has greater symmetry in its neutron placements than does Cu65.
ഀ ഀIf these two stable copper isotopes form in the manner I have suggested, we must conclude that the 11 extra protons that attach to the central 18-proton group will be very hungry for neutrons, since 34 & 36 neutrons are needed to form the neutron "saturated" structures I show below. Hence, these protons must grab most of the neutrons that reside in the two columns that are to the right and left of this center group. Here, then, is the answer to the last of my mystery questions below Table 6. Incidentally, the single-plane structures for copper, below, could very likely not sustain all the alpha groups shown, because they are too much surrounded by nucleons in the six-state charge-exchange. If these alpha groups revert to six-state, the total mass-deficit would be substantially less. Here is another reason to prefer the five-plane structures.
ഀ ഀ
Discussion: If I have reasoned correctly that the stable copper isotopes "prefer" the five-plane form, then we have found another reason to conclude that fractionation route #8 will not occur, in addition to the implausibility of thorium splitting into four equal pieces: there won't be enough released mass-energy to achieve separation! Of course, the inability of the copper group to release gross amounts of mass-energy by converting to single-plane form does not prevent thorium from fractionating 4-Ti/1-Cu, since the splitting off of the four titanium groups leaves the copper group isolated, whereupon it simply converts into one of the five-plane structures shown above.
ഀ ഀI obtained the information about the "Cincinnati Disclosure" from a research note on Harold Aspden's website (http://www.energyscience.org.uk/notes/rn9714.htm). I have not read the original article in the March-June 1997 Double Issue (Nos. 13 & 14) of 'Infinite Energy', although I will. What particularly interests me is whether this low-energy electrolytic fissioning process will work with other radioactive nuclei, and render them similarly harmless, as the Cincinnati Group expects, or whether the structural attributes of thorium are unique, or perhaps shared by only a few other nuclei. I hope to report on this investigation in a few months.
ഀ ഀMeanwhile, there are endless complexities still to be mastered in my theory, and many assertions on my website still to be tested, and perhaps to be refuted. I welcome your comments. My e-mail address is on my website.
ഀ ഀREFERENCES
ഀ ഀ ഀ ഀ ഀ