In QCD, hadrons are postulated to be combinations of either two quarks (a matter/antimatter pair, termed a meson), or a combination of three quarks, termed a baryon (all three quarks being either of matter, or of antimatter flavor). Quarks are defined as fundamental sub-particles comprising a family of 36 members, which differ in flavor, charge, color, mass, and matter/antimatter valences. Let us explore what is meant by each of these quark properties:
Flavor is the most fundamental way that quarks are classified. There are six flavors of quarks: down, up, strange, charm, bottom & top; and six flavors of anti-quarks: the same six, but with an "anti-" prefix. These flavors are normally abbreviated as follows:
| _ | _ | _ | _ | _ | _ | ||||||
| d, | u, | s, | c, | b, | t, | d, | u, | s, | c, | b, | t |
Further references in the website or book to these antimatter quarks, and other antimatter particles, will be prefaced by "@"; hence, @d, @u, @s, @c, @b, @t.
The first two flavors, d & u, are the only ones needed to describe ordinary hadron matter, i.e. protons (uud) & neutrons (udd). The other three flavors of quarks & antiquarks were gradually added over the years as new classes of particles were discovered. (None of these new particles required the t-quark; it was added to the list simply because the b-quark looked lonely without a partner analogous to u & c). Hundreds of kinds of these transient hadron resonances are now known, and their numbers continue to grow.
These resonances vary in mass from pions (»137 MeV) & nucleons (»939 MeV) to upsilon mesons (9640 to 11020 MeV). The search for analogous top quark combinations has been under way for over a decade in increasing mass regions, with no success until recently, when Fermilab announced finding a structure at 160 - 170 GeV that was assumed to be a t@t meson. This mass for the t-quark is so much higher than anyone expected, that, in my appraisal, it should be considered to be a new phenomenon, perhaps a second generation of W & Z particles (these are considered micro-black-holes in infinite particle physics).
An obvious difficulty for the student of QCD is that all quarks, regardless of flavor, or color, are assumed to be infinitesimal points. He must try to understand how 36 varieties of structureless points can differ in flavor, color, mass, charge, bonding propensities, and decay modes, and yet all possess the same spin. He obviously can't!
IPP's defect-pairs, like QCD's quarks, can exist in a large number of "flavors". However, unlike quarks, which all have the same structure (a point) and indefinite mass, each of IPP's defect-pair "flavors" has a specific defect-spacing, which can be drawn to scale, and a specific mass, which can be calculated by a simple formula. These defect spacings will always be integers of the space-lattice constant, and will always be an odd number of lattice units for paired like-charge c-voids, and an even number, for paired opposite-charge c-voids.
When we view particles, resonances, and nuclei, as clusters of defect-pairs, we find that we can understand their qualitative and quantitative aspects by classifying the various defect-pair configurations into the following four variable parameters:
Charge-exchanges between face-diagonally adjacent c-voids: We shall find compelling arguments which persuade us that, in many defect-pair clusters, charges of opposite polarity often exchange places between adjacent orthogonal defect-pairs. For example, the four +1/2e c-voids and the two –1/2e c-voids comprising the three mutually orthogonal defect-pairs of the proton undergo a repetitive cycle of six charge-exchanges, which causes each c-void site to change charges in the following sequence: +, +, +, +, –, –. Each site, of course, begins this endlessly-repeated sequence at a different point in the charge-exchange cycle. Charge-exchanges greatly prolong the lifetime of defect-pair clusters, compared to those lacking charge-exchange opportunities, by muting the disrupting influence of passing charged voids, and other charged destabilizing agents.
Inter-defect-pair bonds: One of the most persuasive aspects of the defect-pair concept for hadron particles is its ability to explain strong-force bonds, without the need for any auxiliary agents, such as QCD's gluons. The bonding between defect-pairs is merely a lesser manifestation of the same process which binds paired c-voids together, namely, suitable alignments of adjacent defect-pairs that permit further cancellations of expansion/contraction distortion. This is possible, because every paired c-void is surrounded by uncanceled residues of expansion/contraction distortion, simply because, being spaced apart, each c-void sees the inverse-square attenuated distortion pattern of its mate. It should be evident that these inter-defect-pair cancellations require opposite "slants", and precise lattice orientations, if bonds are to develop between adjacent c-voids of the two defect-pairs. These geometrical constraints account for the short range of "strong-force" bonds. They also allow one to infer the most plausible structures for defect-pair clusters and nuclei.
Some general conclusions: IPP shows that all hadron resonances, regardless of mass-energy, can be described as clusters of one, or more, defect-pairs. Clusters can form in one, two, or three-axis arrangements, which can assume a great variety of geometrical configurations. These clusters are bound together either by inter-defect-pair charge-exchanges, or by inter-defect-pair strong-force bonds, or by both. What permits this one building-block, defect-pairs, to produce structures whose mass-energies range from pions (136, 139 MeV) to upsilons (9460 ® 11020 MeV), is that both the defect-spacings and defect-pair mass-energies tend to increase with cluster complexity. Under VISUAL IMAGES, I provide many examples of explicit meson and baryon structures. We shall find that these structures correlate nicely with the charge-forms, parities, symmetries, and experimental mass-energy values of numerous resonances inferred from the analysis of high-energy particle experiments.
Charge is an ad hoc concept in QCD. Charges are assigned to the sixty-two "fundamental" particles without reference to an underlying source, or concept, of charge. Obviously, the fact that charge is conserved in all observed particle creations and decays guides these charge assignments, but QCD theory makes no attempt to correlate charge differences with differences in lepton, or quark, structures. QCD assigns ± e charges to its three classes of leptons (± electrons, ± muons, & ± taus), but its three classes of neutrinos are presumed to have neutral charges (whatever that is!). Its quark charges, on the other hand, are presumed to be fractional, as outlined below.
Fractional quark charges of ± 1/3e & ± 2/3e were conceived initially as simply a clever mathematical scheme to make two-quark & three-quark particles sum to the observed particle charges of - 2e, - e, 0, + e, + 2e. The ± 2e charges, of course, are possible only to three-quark particles. This scheme was perhaps put on a firm experimental basis, when high-energy electron scattering experiments on protons were interpreted as showing a + 1/3e charge in this + e charge particle, in which the electron presumably grazes two quarks, d & u, whose charges sum to + 1/3e (see below). I give IPP's interpretation of this experiment later in the book. Now let us look at the charges that QCD assigns to its flavors of quarks:

The anti-quarks have the same values, but with opposite signs. One should note that QCD makes no effort to explain what charge is, nor why quark charges are different from lepton charges, ± e & 0.
IPP requires only two fundamental charge forms: These are the postulated ± 1/2e "charges" of the elemental charge entities (ECEs) comprising the polycrystalline lattice of space. No other charges need be assigned, because the charges of all the various leptons and hadrons are implicit in their associated defect structures. Every specific particle type has a unique defect structure at its center, and each defect, or combination of defects, results in a calculable imbalance in the local numbers of + ECEs vs. - ECEs. Hence, one obtains the charge of a particular particle simply by summing the charges of the number of excess ECEs present (zero charge is obviously possible, if the mix of defects creates zero imbalance).
Like QCD, IPP can offer no explanation for the "charges" of its fundamental particles, ECEs, but it does provide geometric explanations for the charges of all observed particles, including neutral "charges", without the need to postulate any other charge forms.
Rather than QCD's way of thinking of antimatter as some strange beast, happy only in an antimatter universe, IPP views antimatter as simply a clustering of defects whose charges are opposite to those of ordinary matter. Defects, and charged defect-clusters, of the same defect composition can have two charge forms, either plus, or minus. The infinitely-extending lattice-distortion patterns of these opposite charge forms will resemble each other in all particulars, except for one thing: every corresponding ECE in their infinite patterns will be of opposite polarity! This is how IPP differentiates matter from antimatter.
Color is a bookkeeping term that is used to make QCD conform to the Pauli Exclusion Principle. Its necessity is inferred from a chain of reasoning beginning with assigning quarks a spin of 1/2, so that a proton's three quarks (uud) can sum to its known spin of 1/2 (by assigning opposite spins to the two u-quarks). The next step in the chain resulted from finding several resonances whose measured spins were 3/2, and whose quark components were required to be all of the same flavor, like omega– (ccc), delta– (ddd), & delta++ (uuu).
Because physicists currently believe that all odd-spin particles are expected to obey Pauli's Exclusion Principle, the only way that a cluster of three like-flavor quarks of 1/2 spin can sum to a spin of 3/2 is for all of them to be different in some unspecified characteristic; hence, each quark must come in three "colors", and each anti-quark must come in three "anti-colors"! Then to justify this deduction, QCD asserts that all other combinations of three quarks need to have one member from each of the three quark color values, and, hence, be "color neutral". Likewise, each two-quark particle must also be "color neutral", which requires that its anti-quark be the anti-color of its quark mate.
IPP, on the other hand, perceives the spin of particles as resulting from three effects: hovering, charge-exchanges and orientation isomers. Hovering and charge-exchanges introduce detectable wobble in the center locations of a particle's distortion pattern, while orientation isomers are detectable as spin, only through their differential deflections in particle detectors, or in Stern-Gerlach apparatus. Orientation isomers may be defined as asymmetrical clusters of identical defect-pair composition, which have formed in a variety of spatial orientations. It is evident that a cluster's asymmetry can assume at least three orientations in space (and often more), because any particular defect-pair in a cluster can orient in any of the three cardinal directions of the space lattice.
Thus, in contrast to QCD, IPP has no need for Pauli's Exclusion Principle in its study of particle structures, because IPP interprets particle spins as a structural feature, not a component feature.
Mass is QCD's Achilles heel. There is no direct way to weigh a quark, because quarks are assumed never to be found in isolation. Rather, quarks are presumed to exist only as sub-components of larger hadron entities classified into two varieties, mesons and baryons. Since the quark components and accurate masses of dozens of particles and resonances are known (i.e. have been assigned), it would seem to be an easy problem to extract the quark masses from this data, but, alas, there are complications! I give a few examples below, to illustrate the problem:
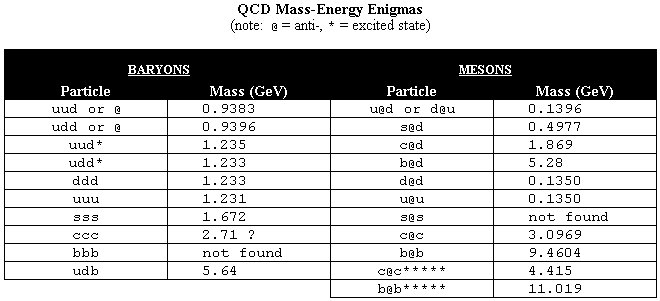
Here are some things the this chart reveals:
QCD's solution to these obvious inconsistencies is to postulate that an uncombined quark (a "naked" quark) has a small mass, but this mass is greatly augmented when the quarks are in a combined state with other quarks. Thus, one must extrapolate backwards from various spectrums of excited particle states to find a value for a "naked" quark. These extrapolations are esoteric and do not fit all excited particle spectrums equally well, so many have been proposed. Thus, these "naked" quark masses for the various flavors of quarks can be given only as a range of values. Here are the values given in LBL 2000 Review of Particle Properties, page 26:

In IPP, mass-calculations are straightforward:
IPP views QCD's excited particle states as structures of similar geometry to the ground state, but with either different defect-pair spacings, or with different strong-force bond spacings, or with both. IPP's concept of an excited state is simply one in which analogous defect-pair spacings are larger than those of the ground state, or analogous bonds spacings are smaller (or both).
There is nothing equivocal about IPP's hadron structures, since both the inferred defect-pair spacings and bond spacings are quantized phenomena. Hence, IPP's mass calculations, when compared against experimental values, are a valid test of the Theory.
QCD tantalizes us by assigning quantum numbers to each well-validated resonance. These quantum numbers are an abstract specification of the symmetry, spin, parity, strangeness, etc., of a resonance, as determined from its observed decay modes, e.g., whether it decays symmetrically, or asymmetrically, what charge imbalance exists in decay products, etc. We get only a fuzzy picture of its structure, something the mind cannot grasp as a clear image. Furthermore, we may get a false impression, because symmetrical resonances may manifest asymmetrical decays, as IPP is able to demonstrate!
IPP provides accurately scaled, three dimensional diagrams of mesons and baryons, which show the number of defect-pairs, their internal defect spacings, and their geometric relationships and bond spacings. These diagrams usually show all the charge-exchange states of the particle's complete charge-exchange cycle. Since all the inter-defect spacings are integer numbers of lattice units (ü), precise mass calculations can be made. These frequently correlate within ±0.01% for resonances whose mass values are accurately known.
The greatest contrast between QCD and IPP is not between quarks and defect-pairs. It is, rather, in the basic concepts of particles, themselves.
QCD theorists consider hadron particles to be composed of either two infinitesimal quarks (mesons), or three infinitesimal quarks (baryons). They believe that the quarks comprising these hadron particles can assume different identities, such as different flavors, colors, charges, masses, and degrees of excitement, and that a limited number of these different identities are sufficient to explain all the well-validated mesons & baryon resonances inferred from accelerator experiments. Their proof for this belief is expressed in various classification schemes. To see the details of these Quark classification schemes, please click here.
IPP theorists, on the other hand, view hadron particles as dynamic point-centered infinitely extending lattice distortion patterns centered upon clusters of defect pairs. They believe that defect-pairs can form at various inter-defect spacings, in various cardinal directions, slants, geometric arrangements, and in numbers up to sixteen per cluster, and this variety is sufficient to explain all known resonances and even those yet to be discovered. Their goal is to find a unique geometrical arrangement of clustered defects for each distinguishable particle or resonance, and prove that it matches its experimental mass-energy and charge values. These correlations in IPP are shown as an animated sequence of accurately-scaled 3-D drawings of all the particle's charge-exchange states, along with an animated sequence of individual mass-energy calculations for each state, their simple average, and the experimental mass-energy value. The cluster's charge is easily perceived, as the summation charge of all the color-coded ± 1/2e charges of the component c-void defects.
The differences between these two approaches can also be explored, philosophically, to rather interesting conclusions. I do this in the next section.
Let's begin by imagining that we haven't yet made up our minds about these two alternatives. What do we already know that could be used as evidence for attesting to the validity (or usefulness) of either viewpoint? Let's lay out this evidence:
If particles are assumed to be infinitesimal points:
* This value obtained from Institute of Physics website, Science Museum (1997).
This extreme cosmic emptiness raises four serious theoretical difficulties:If particles are assumed to be infinitely large, current theoretical difficulties largely disappear:
I hope that you have found these comparisons between QCD and IPP useful to your study of Infinite Particle Physics. To continue, please choose any item from the Navigation Bar to your left.